
The main interest in my research is the intersection of gravitation and astronomy. In particular, I am interested in testing theories that modify gravity by using a different dependence on the curvature scalars in the Hilbert-Einstein action. Recently, we proposed a new theory that adding an infinite series of higher curvature invariants can provide second-order equations for a homogeneous and isotropic universe with a well-defined initial value problem. Within this frame, it is possible to produce an inflationary period with graceful exit and late time acceleration. I am also interested in the predictions of this theory regarding stars. Currently, we are also developing a research program to investigate different alternatives for late-time acceleration, the ones coming from scalar fields and those coming from gravity modifications like f(R).
Luisa G. Jaime
Astrophysicist
MY LATEST RESEARCH
A unified geometric description of the Universe: From inflation to late-time acceleration without a cosmological constant.
Luisa G. Jaime & Gustavo Arciniega.
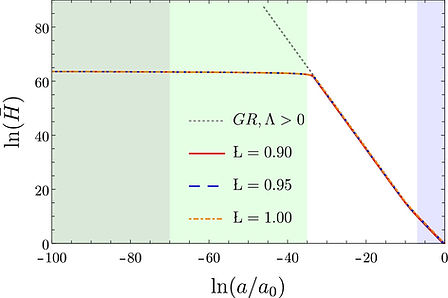
We present a cosmological model arising from a gravitational theory with an infinite tower of higher-order curvature invariants that can reproduce the entire evolution of the Universe: from inflation to late-time acceleration, without invoking an inflaton nor a cosmological constant. The theory is Einsteinian-like. The field equations for a Friedmann-Lemaître-Robertson-Walker metric are of second-order and can reproduce a late-time evolution that is consistent with the acceleration provided by the cosmological constant at low redshift. Our results force us to reinterpret the nature of dark energy, becoming a mechanism that is inherited solely from the geometry of spacetime
One parameterisation
to fit them all.
Gustavo Arciniega, Mariana Jaber, Luisa G. Jaime & Omar Rodríguez
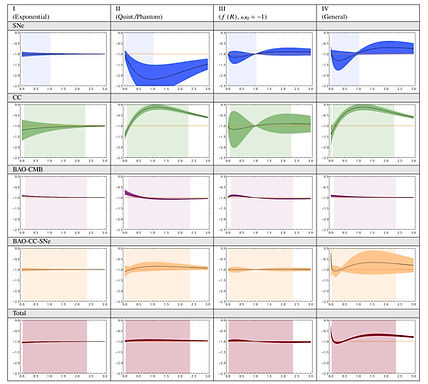
We present a parametric form for ω(z) that can reproduce the generic behaviour of the most widely used physical models for accelerated expansion with infrared corrections. The present proposal has at most 3 free parameters which can be mapped back to specific archetypal models for dark energy. We analyze in detail how different combinations of data can constrain the specific cases embedded in our form for ω(z). We implement our parametric equation for ω(z) to observations from CMB, luminous distance of SNeIa, cosmic chronometers, and baryon acoustic oscillations identified in galaxies and in the Lymann-α forest. We find that the parameters can be well constrained by using different observational data sets. Our findings point to an oscillatory behaviour which is consistent with an f(R)-like model or an unknown combination of scalar fields. When we let the three parameters vary freely, we find an EOS which oscillates around the phantom-dividing line, and, with over 99% of confidence, the cosmological constant solution is disfavored.